Most investors are familiar with the Rule of 72, a formula for approximating the time it takes an investment to double at a given compounded annual return. The Rule states that dividing 72 by the annual return equals the number of years to double. Conversely, the Rule of 72 can also determine the annual return by dividing 72 by the number of years. For example, it takes nine years to double an investment compounding at 8% a year (72/8% = 9 years). Similarly, the return required to double an investment in just six years is 12% (72/6 years = 12%).
Retirement is the primary goal of many investment plans. These long-range plans require more than just a doubling of an investment and involve time horizons that are longer than those easily estimated with the Rule of 72. To make the planning process easier, I developed the Rule of 240, a formula for approximating the time and/or compounded return needed for an investment to increase by a factor of ten. The mathematical term for a factor of ten is called an “order of magnitude” and it may be easier to think about it as “adding a zero” to your investment. The methodology for using the Rule of 240 is the same as the Rule of 72.
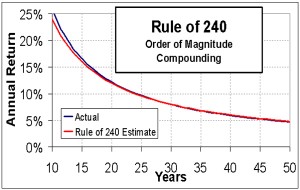 Namely, the number of years it takes to increase an investment by an order of magnitude, multiplied by the annual return is equal to 240. For example, an investment will take 20 years to add a zero ($100 will grow to $1,000) if the return is 12% a year (240/12% = 20 years). With an 8% annual return, it will take an investment 30 years to increase by a factor of ten.
Namely, the number of years it takes to increase an investment by an order of magnitude, multiplied by the annual return is equal to 240. For example, an investment will take 20 years to add a zero ($100 will grow to $1,000) if the return is 12% a year (240/12% = 20 years). With an 8% annual return, it will take an investment 30 years to increase by a factor of ten.
Although the Rule of 240 is an estimation technique, it is a reasonably accurate estimate. The Rule of 240 is accurate to within six months for all returns in the 6% to 15% range and is accurate to within 0.1% a year for all periods greater than 21 years.